電圧逓倍回路について
コッククロフト回路が有名です。

一倍回路	入力電圧が出力電圧です。ダイオードの順方向電圧分の降下があります。
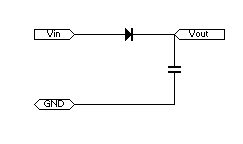
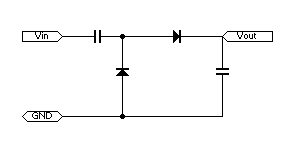
二倍回路	俗に言う「半波倍電圧整流回路」ですが・・・これ大嘘です。 一倍回路で電力を利用しないサイクルでコンデンサをチャージしています。 立派に”両波”利用回路です。 そんな訳でこの回路では入力はＡＣでなければいけません。 プラスだけのパルス列では入力電圧が出てくるだけでなく、入力側のコンデンサが ムダに充放電を繰り返します。（しかもＡＣを与えた場合とは逆方向なので極性あるコンデンサである場合は寿命に影響します） プラス側だけのパルスや脈流で入力電圧の倍を得るには・・・ これで入力電圧の倍の電圧が得られるでしょう。（ＡＣを与えたら３倍になります）
３倍回路	二倍回路の描き方をちょっと変えます。 これを一倍回路に乗せたモノが３倍回路となります。 ３倍回路は、ＡＣでもパルスでも動作します。しかしパルスでは電力が半分しか 注入されない事になるので、倍にしかなりません。
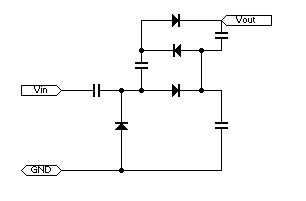
４倍回路	二倍回路に乗せた状態です。 パルス入力では２倍弱の出力しか得られません。入り口のコンデンサが苛められるのでこの回路にパルスを与えることは意味がありません。
５倍回路	３倍回路に乗せました。 ＡＣ入力で５倍の出力電圧が得られます。パルス入力では３倍の出力電圧となります。 このように好きなだけ乗せることが出来ます。 ４倍回路のところで説明した事情により６倍回路にパルス入力すると３倍弱の出力電圧しか得られません。

コンデンサの容量は同じで揃えるのが簡単です。極端に変えると出力電圧はむしろ下がります。


上記の回路ではＡＣが無い時は逓倍率が低いモノですが、デューティ五割のパルスが得られるなら面白い回路があります。
この回路も同じ容量のコンデンサで十分です。容量を変えても改善度は低いです。

ｎを[ダイオードの数] として( n>=3) Ａ点をＶｃｃに接続するとＢ点には（Ｖｃｃ−Ｖｆ）＊ｎ の電圧が得られます。 Ｂ点をＧＮＤに接続するとＡ点には Vf−（Ｖｃｃ−Ｖｆ）＊(ｎ-1)　の電圧が得られます。 段数の増減はダイオードとコンデンサのペア単位で行います。 正・補の段数が揃わなくても構いません。